无目的读书是散步而不是学习

LLAA Home

A_Neurobiology_003_MembranePotential

发布于 # neuroscience • #Neuroscience

Resting Membrane Potential

可兴奋的细胞不产生冲动时，称为静息状态；处于静息状态的神经元膜内相对于膜外是负电荷，跨膜电荷存在着差异称为resting membrane potential

The Chemical Basis

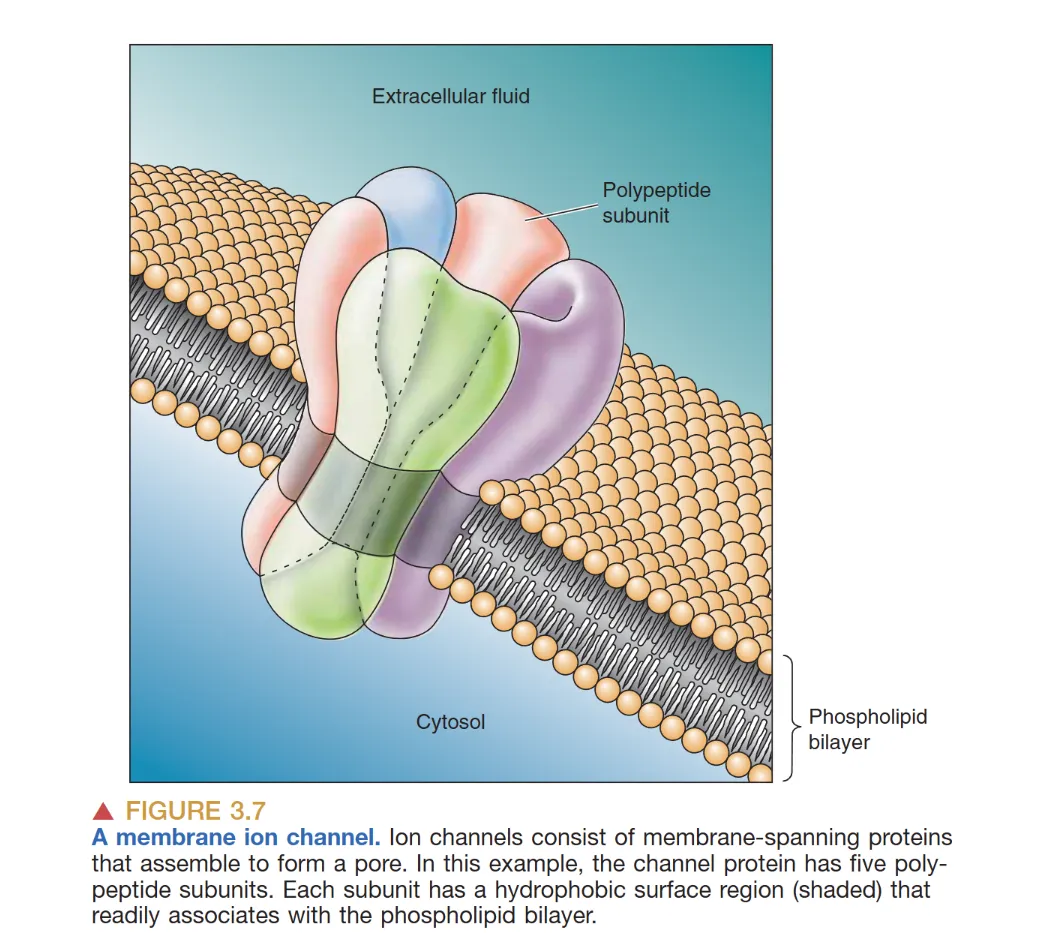
Movement of Ions

  1. 扩散: 通过离子通道顺浓度梯度扩散。
  2. 电场驱动: Movement of ions due to an electrical field (Current II, Voltage VV, Conductance gg).

Ion Basis of RMP

Nernst Equation

Eion=2.303RTzFlog[ion]o[ion]iE_{ion}=2.303\frac{RT}{zF}log\frac{[ion]_o}{[ion]_i}

这里E为某个离子的静息膜电位。 K+: in>out Na+ Ca2+ Cl-: out>in

[!note] 37°C 时的简化公式

Eion=61.65zlog[ion]o[ion]iE_{ion}=\frac{61.65}{z}log\frac{[ion]_o}{[ion]_i}
离子浓度比 (外:内)平衡电位 (EionE_{ion})
K+K^+1 : 20-80 mV
Na+Na^+10 : 1+62 mV
Ca2+Ca^{2+}10,000 : 1+123 mV
Cl−Cl^-11.5 : 1-65 mV

GHK Equation

Nernst方程只考虑了单个离子如何流动，但细胞膜的离子是复杂的，所以GHK方程在Nernst方程基础上进行了拓展。

GHK Equation

The GHK equation is a fundamental fomula in neuroscience, extending the Nernst equation which is limited to a single ion species. It considers the relative permeabilities and concentrations of multiple ions.

Assumptions

Because the environment in the cell is very complex, we must build some assumptions to make the deriving process easy.

step1 Get the JiJ_i equation about CioutsideC_i^{outside}and CiinsideC_i^{inside}

From Nernst-Planck Equation：

Ji=−Di(dCidx+ziFRTCidVdx) J_i=-D_i(\frac{dC_i}{dx}+\frac{z_iF}{RT}C_i\frac{dV}{dx})

Apply the Constant Field Assumption: Because of the assumption: dVdx=−Vmd\frac{dV}{dx}=-\frac{V_m}{d} where Vm=Voutside−VinsideV_m=V_{outside}-V_{inside} so, substitute dVdx\frac{dV}{dx} into the Nernst-Planck Equation: define α=ziFRTdVm\alpha=\frac{z_iF}{RTd}V_m

Ji=−Di(dCidx−αCi) J_i=-D_i(\frac{dC_i}{dx}-\alpha C_i)

here, we time e−αxe^{-\alpha x} on both sides:

∵e−αxJi=−Di(dCidxe−αx−αeαxCi)∴−e−αxJiDi=dCidxe−αx−αe−αxCi∴−e−αxJiDi=∂(Cie−αx)∂x\begin{aligned} \because e^{-\alpha x}J_i=-D_i(\frac{dC_i}{dx}e^{-\alpha x}-\alpha e^{\alpha x}C_i) \\ \therefore -\frac{e^{-\alpha x}J_i}{D_i}=\frac{dC_i}{dx}e^{-\alpha x}-\alpha e^{-\alpha x}C_i\\ \therefore -\frac{e^{-\alpha x}J_i}{D_i}=\frac{\partial (C_ie^{-\alpha x})}{\partial x} \end{aligned}

Now, we can integrate both sides from x=0(inside)x=0(inside) to x=d(outside)x=d(outside)

−JiDiα∫x=0x=de−αxdx=(Cie−αx)∣x=0x=d∴Ji(e−αd−1)Diα=Cioe−αd−Cii∴Ji=−Diα(Cio−Ciieαd)eαd−1\begin{aligned} -\frac{J_i}{D_i\alpha}\int_{x=0}^{x=d}e^{-\alpha x}dx=(C_ie^{-\alpha x})\mid_{x=0}^{x=d}\\ \therefore \frac{J_i (e^{-\alpha d}-1)}{D_i \alpha}=C_i^oe^{-\alpha d}-C_i^i\\ \therefore J_i=-\frac{D_i\alpha(C_i^o-C_i^ie^{\alpha d})}{e^{\alpha d}-1} \end{aligned}

We use CioC_i^o and CiiC_i^i to represent the concentration of the given ion inside and outside the membrane. Then recall that α=ziFVmRTd\alpha=\frac{z_iFV_m}{RTd}, and substitute Did=Pi\frac{D_i}{d}=P_i (represent the permeability of ion ii)

Ji=−PiziFVm(Cio−CiieziFVmRT)RT(eziFVmRT−1)\begin{aligned} J_i=-\frac{P_i{z_iF}V_m(C_i^o-C_i^ie^{\frac{z_iFV_m}{RT}})}{RT(e^{\frac{z_iFV_m}{RT}}-1)} \end{aligned}

We use ξi=ziFVmRT\xi_i=\frac{z_iFV_m}{RT}, so we can get:

Ji=−PiξiCio−Ciieξieξi−1\begin{aligned} J_i=-P_i\xi_i\frac{C_i^o-C_i^ie^{\xi_i}}{e^{\xi_i}-1} \end{aligned}

Step2 get VmV_m

The ionic current IiI_i per square is

Ii=ziFJi∴Ii=−Pizi2F2Vm(Cio−Ciieξi)RT(eξi−1)\begin{aligned} I_i=z_iFJ_i\\ \therefore I_i=-\frac{P_i{z_i^2F^2}V_m(C_i^o-C_i^ie^{\xi_i})}{RT(e^{\xi_i}-1)} \end{aligned}

Apply IiI_i to the Steady-State Condition, where

∑Ii=Itotal=0\sum I_i=I_{total}=0

we use K+K^+, Na+Na^+ and Cl−Cl^- as examples, which are significant for the membrane potential. Here it is:(let ξ=FVmRT\xi=\frac{FV_m}{RT})

IK+=−PK+F2Vm(CK+o−CK+ieξ)RT(eξ−1)INa+=−PNa+F2Vm(CNa+o−CNa+ieξ)RT(eξ−1)ICl−=−PCl−F2Vm(CCl−o−CCl−ie−ξ)RT(e−ξ−1)=−PCl−F2Vm(CCl−i−CCl−oeξ)RT(eξ−1)\begin{aligned} I_{K^+}=-\frac{P_{K^+}{F^2}V_m(C_{K^+}^o-C_{K^+}^ie^{\xi})}{RT(e^{\xi}-1)}\\ I_{Na^+}=-\frac{P_{Na^+}{F^2}V_m(C_{Na^+}^o-C_{Na^+}^ie^{\xi})}{RT(e^{\xi}-1)}\\ I_{Cl^-}=-\frac{P_{Cl^-}{F^2}V_m(C_{Cl^-}^o-C_{Cl^-}^ie^{-\xi})}{RT(e^{-\xi}-1)}\\ =-\frac{P_{Cl^-}{F^2}V_m(C_{Cl^-}^i-C_{Cl^-}^oe^{\xi})}{RT(e^{\xi}-1)} \end{aligned}

So the sum of the currents is

∑Ii=IK++INa++ICl−=0\sum I_i=I_{K^+}+I_{Na^+}+I_{Cl^-}=0

substitute the currents:

−PK+F2Vm(CK+o−CK+ieξ)RT(eξ−1)−PNa+F2Vm(CNa+o−CNa+ieξ)RT(eξ−1)−PCl−F2Vm(CCl−i−CCl−oeξ)RT(eξ−1)=0⇒PK+CK+o+PNa+CNa+o+PCl−CCl−i=eξ(PK+CK+i+PNa+CNa+i+PCl−CCl−o)∴eξ=PK+CK+o+PNa+CNa+o+PCl−CCl−iPK+CK+i+PNa+CNa+i+PCl−CCl−o\begin{aligned} -\frac{P_{K^+}{F^2}V_m(C_{K^+}^o-C_{K^+}^ie^{\xi})}{RT(e^{\xi}-1)}-\frac{P_{Na^+}{F^2}V_m(C_{Na^+}^o-C_{Na^+}^ie^{\xi})}{RT(e^{\xi}-1)}-\frac{P_{Cl^-}{F^2}V_m(C_{Cl^-}^i-C_{Cl^-}^oe^{\xi})}{RT(e^{\xi}-1)}=0\\ \Rightarrow P_{K^+}C_{K^+}^o+P_{Na^+}C_{Na^+}^o+P_{Cl^-}C_{Cl^-}^i=e^{\xi}(P_{K^+}C_{K^+}^i+P_{Na^+}C_{Na^+}^i+P_{Cl^-}C_{Cl^-}^o)\\ \therefore e^{\xi}=\frac{P_{K^+}C_{K^+}^o+P_{Na^+}C_{Na^+}^o+P_{Cl^-}C_{Cl^-}^i}{P_{K^+}C_{K^+}^i+P_{Na^+}C_{Na^+}^i+P_{Cl^-}C_{Cl^-}^o} \end{aligned}

recover ξ\xi with FVmRT\frac{FV_m}{RT}

Vm=RTFlnPK+CK+o+PNa+CNa+o+PCl−CCl−iPK+CK+i+PNa+CNa+i+PCl−CCl−oV_m = \frac{RT}{F}ln\frac{P_{K^+}C_{K^+}^o+P_{Na^+}C_{Na^+}^o+P_{Cl^-}C_{Cl^-}^i}{P_{K^+}C_{K^+}^i+P_{Na^+}C_{Na^+}^i+P_{Cl^-}C_{Cl^-}^o}

Vm=ECl=−65mVV_m=E_{Cl}=-65mV 通透性与离子通道开放的个数有关，在RMP与AP下，通透性不同，所以膜电位也会相应改变 P*K:P_na:Pcl At rest PK:P∗Na:P∗cl=1:0.04:0.45P_K:P*{Na}:P*{cl} = 1:0.04:0.45 Action potential PK:P∗Na:P_cl=1:20:0.45P_K:P*{Na}:P\_{cl} = 1:20:0.45